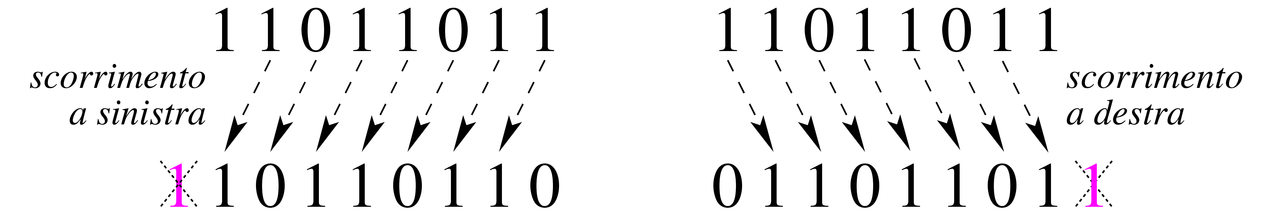Operazioni logiche su numeri binari
Operatori logici (logical operators)
A livello di singolo bit, definiamo tre operatori fondamentali (NOT, AND, OR), più un quarto operatore molto comune (XOR), per mezzo delle loro TruthTables (tabelle della verità):
NOT (¬) o negazione logica x | ¬ x --+----- 0 | 1 1 | 0 |
AND (∧) o prodotto logico x y | x∧y ----+----- 0 0 | 0 0 1 | 0 1 0 | 0 1 1 | 1 |
OR (∨) o somma logica x y | x∨y ----+----- 0 0 | 0 0 1 | 1 1 0 | 1 1 1 | 1 |
XOR (⨁) o somma modulo 2 x y | x⨁y ----+----- 0 0 | 0 0 1 | 1 1 0 | 1 1 1 | 0 |
Una forma condensata della tabella di verità è usata per gli operatori binari; in questa, i titoli delle righe e colonne indicano gli operandi, e gli elementi della matrice il risultato. L'algebra di Boole, ad esempio, usa questa notazione condensata della tabella della verità:
NOT
| AND
| OR
| XOR=(¬X ∧ Y) ∨ (X ∧ ¬Y)
|
Questa notazione è utile specialmente se gli operatori sono commutativi, benché si possano specificare le righe come primo operando e le colonne come secondo. La notazione abbreviata è particolarmente utile quando si trattano valori logici multipli, dato che rallenta il vertiginoso aumento di righe che sarebbe altrimenti necessario usare. Fornisce anche una forma caratteristica e prontamente riconoscibile della distribuzione dei valori nella tabella, permettendo al lettore una più rapida comprensione.
Operatori bit a bit (bitwise operators) su numeri binari e decimali
I bitwise operators lavorano su schemi di uno o più bit o su numerali binari al livello dei loro bit individuali. Si tratta di azioni primitive, veloci, supportate direttamente dal processore, e sono usate per manipolare valori per il confronto e il calcolo. In processori a basso costo è una operazione tipica, più veloce della divisione, diverse volte più veloce della moltiplicazione, e talvolta significativamente più veloce dell'addizione. Mentre i processori moderni di solito eseguono addizione e moltiplicazioni come un'operazione bit a bit veloce dovuto alle più lunghe instruzioni pipeline e altre scelte di progettazione architetturale, le operazioni bit a bit sono più comuni a basse prestazione per il loro ridotto uso di risorse.NOT (oppure Negazione logica)
L'operazione bit a bit di NOT, o complemento a uno (indicata in alcuni linguaggi di programmazione con ~), è una operazione unaria che esegue la negazione logica su ogni bit, formando l'uno complemento sul valore binario dato. Bit che sono 0 diventano 1, e quelli che sono 1 diventano 0. Per esempio:60 --> 00111100 ----------------------- ~a --> 11000011 è uguale a 195 in decimale (C3 in esadecimale).A livello di singolo bit, gode delle seguenti proprietà:
- ~~x=x
AND (oppure et oppure Congiunzione logica oppure prodotto logico)
L'operazione bit a bit AND (indicata in alcuni linguaggi di programmazione con &), esegue un confronto tra due variabili dando come risultato una terza variabile in che presenta '1' in quei posti in cui entrambe le variabili di partenza presentano 1 e '0' in tutte le altre.60 --> 00111100 240 --> 11110000 ----------------------- a&b --> 00110000 è uguale a 48 in decimale (30 in esadecimale).A livello di singolo bit, gode delle seguenti proprietà:
- idempotenza x&x=x
- associativa (x&y)&z=x&(y&z)
- commutativa x&y=y&x
- esistenza elemento neutro x&1=x
- esistenza elemento assorbente x&0=0
- esistenza elemento "inverso" x&~x=0 (ma l'elemento neutro è 1!)
- distributiva rispetto all'OR (e rispetto allo XOR)
OR (oppure vel oppure Disgiunzione inclusiva oppure Somma logica)
L'operazione bit a bit OR (indicata in alcuni linguaggi di programmazione con |), esegue un confronto tra due variabili dando come risultato una terza variabile che presenta '1' in quei posti in cui almeno una delle due variabili presenta 1 e setta a '0' tutti gli altri posti (ossia tutti i posti in cui entrambe le variabili presentano '0'. Potrebbe considerarsi come l'operazione simmetricamente opposta dell'AND di cui sopra.60 --> 00111100 240 --> 11110000 ----------------------- a|b --> 11111100 è uguale a 252 in decimale (FC in esadecimale).A livello di singolo bit, gode delle seguenti proprietà:
- idempotenza x|x=x
- associativa (x|y)|z=x|(y|z)
- commutativa x|y=y|x
- esistenza elemento neutro x|0=x
- esistenza elemento assorbente x|1=1
- esistenza elemento "inverso" x|~x=1 (ma l'elemento neutro è 0!)
- distributiva rispetto all'AND
XOR (oppure aut oppure Disgiunzione esclusiva oppure Somma modulo 2)
L'operazione bit a bit XOR (indicata in alcuni linguaggi di programmazione con ^), esegue un confronto tra due variabili dando come risultato una terza variabile che presenta '1' in quei posti in cui le due variabili presentano valori con valori diversi e settando a '0' tutti gli altri posti.60 --> 00111100 240 --> 11110000 ----------------------- a^b --> 11001100 è uguale a 204 in decimale (CC in esadecimale).A livello di singolo bit, gode delle seguenti proprietà:
- associativa (x^y)^z=x^(y^z)
- commutativa x^y=y^x
- esistenza elemento neutro x^0=x
- esistenza elemento inverso x^x=0
- distributiva rispetto all'AND
- x^1=~x
- x^~x=1
Operazioni di scorrimento logico (Logical shifting, numeri senza segno)
L'operazione di shifting (indicata in alcuni linguaggi di programmazione con << o >>) costituisce una interessante tecnica per effettuare moltiplicazioni o divisioni a bassissimo costo.Scorrimento logico a sinistra
Sposta ciascun bit di una posizione verso sinistra; il bit più significativo esce e viene posto nel registro di carry; nel bit meno significativo viene inserito uno 0.Matematicamente, in base 10, uno shift verso sinistra di una cifra corrisponde ad una moltiplicazione per 10.
Analogamente, in base 2, uno shift verso sinistra di un bit è equivalente ad una moltiplicazione per 2. Ad esempio:
60 --> 00111100 ----------------------- a<<1 --> 01111000 è uguale a 120 in decimale (78 in esadecimale); a<<2 --> 11110000 è uguale a 240 in decimale (F0 in esadecimale).
Scorrimento logico a destra
Sposta ciascun bit di una posizione verso destra; il bit meno significativo esce e viene posto nel registro di carry; nel bit più significativo viene inserito uno 0.Matematicamente, in base 10, uno shift verso destra di una cifra corrisponde ad una divisione per 10 [divisione intera, con perdita del resto].
Analogamente, in base 2, uno shift verso destra di un bit è equivalente ad una divisione per 2 [divisione intera, con perdita del resto]. Ad esempio:
60 --> 00111100 ------------------------- a>>1 --> 00011110 è uguale a 30 in decimale (1E in esadecimale); a>>2 --> 00001111 è uguale a 15 in decimale (0F in esadecimale); a>>3 --> 00000111 è uguale a 7 in decimale (07 in esadecimale). Notare la perdita del resto.