Operazioni aritmetiche con i numeri binari

Dopo aver visto, nel paragrafo precedente, com'è definito il sistema binario, vediamo ora come si svolgono le operazioni aritmetiche con i numeri binari. Si possono infatti tranquillamente eseguire addizione, sottrazione, moltiplicazione e divisione nel sistema binario. Prendiamole in esame una per volta. \( Wink \)

Prima di procedere oltre è necessario avere ben chiaro cos'è il sistema binario e, in caso di dubbi, ti basta un click sul link precedente.

Addizione con i numeri binari

Per eseguire la somma tra due o più numeri binari la prima cosa da fare è incolonnarli: per farlo nel modo giusto basta posizionarli uno sotto l'altro partendo dalla prima cifra a destra e facendole corrispondere. Per intenderci: 

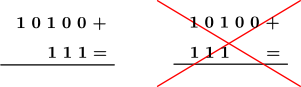
Una volta incolonnati nel modo giusto si esegue la somma dei due numeri binari ricordando che:

\( \begin{array}{c c c c l} 0&+&0&=&0\\ 1&+&0&=&1 \\ 0&+&1&=&1 \\ 1&+&1&=&0 \ \ \mbox{con riporto di 1 alla colonna immediatamente a sinistra} \end{array} \)

Esempi di somma tra numeri binari

Consideriamo la seguente somma secondo il procedimento appena visto

\( \bullet \ (10100)_2 + (111)_2 \ = \ \mbox{?} \)

\( \begin{array}{ccccccc} & {\color{red}1} & & & &\mbox{riporti}\\ 1 & 0 & 1 & 0 & 0 & + \\ & & 1 & 1 & 1 & = \\ \hline 1 & 1 & 0 & 1 & 1\end{array} \)

e abbiamo il risultato: \( (10100)_2 + (111)_2 = (11011)_2 \).

Vediamo un altro esempio. Vogliamo calcolare la somma in base 2

\( \bullet \ (1111)_2 + (1010)_2 + (101)_2\ = \ \mbox{?} \)

\( \begin{array}{ccccccc} 1 & 1 & 1 & 1 & &\mbox{riporti}\\ & 1 & 1 & 1 & 1 & + \\ & 1 & 0 & 1 & 0 & + \\ & & 1 & 0 & 1 & = \\ \hline 1 & 1 & 1 & 1 & 0 & \end{array} \)

quindi il risultato è \( (1111)_2 + (1010)_2 + (101)_2\ = \ (11110)_2 \)

La somma tra numeri binari gode anch'essa della proprietà commutativa e della proprietà associativa.

Sottrazione tra numeri binari

Per eseguire correttamente la differenza tra due numeri binari bisogna innanzitutto incolonnarli così come visto nell'addizione e poi ricordare che:

\( \begin{array}{c c c c c l} 0&-&0&=&0\\ 1&-&0&=&1 \\ 1&-&1&=&0 \\ 0&-&1&=&1& \mbox{dopo essersi prestato 1 dalla colonna a sinistra} \end{array} \)

Attenzione! Quando facciamo un prestito da una colonna ad un'altra, l'unità aumenta il suo valore di uno, cioè è come se ricevessimo in prestito due 1. Sembra difficile da capire ma non è così. Pensate alla sottrazione tra numeri naturali, ad esempio \( 153-45 \). Non potendo eseguire la differenza tra le cifre delle unità, ci presteremo 1 decina, che non equivale ad una bensì a dieci unità.. Insomma: spostandoci di colonna aumenta il valore delle cifre; altra giustifica del fatto che il sistema binario è posizionale. \( Wink \)

Esempi di sottrazione tra numeri binari

\( \bullet \ (11110)_2 - (1010)_2 \ = \ \mbox{?} \)

\( \begin{array}{ccccccc} 1 & 1 & 1 & 1 & 0 & - \\ & 1 & 0 & 1 & 0 & = \\ \hline 1 & 0 & 1 & 0 & 0\end{array} \)

Quindi \( (11110)_2 - (1010)_2 \ = \ (10100)_2 \)

\( \bullet \ (10010)_2 - (1101)_2 \ = \ \mbox{?} \)

\( \begin{array}{ccccccc} \\ 1 & 0 & 0 & 1 & 0 & - \\ & 1 & 1 & 0 & 1 & = \\ \hline 0 & 0 & 1 & 0 & 1\end{array} \)

Pertanto \( (10010)_2 - (1101)_2 \ = \ (101)_2 \)

Prodotto tra numeri binari

Per eseguira la moltiplicazione tra due numeri binari bisogna innanzitutto tener presente che:

\( \begin{array}{c c c c l} 0&\times &1&=&0\\ 1& \times &0&=&0 \\ 0&\times&0&=&0 \\ 1&\times&1&=&1 \end{array} \)

e poi procedere come visto per il prodotto tra numeri naturali, ovvero:

- si incolonnano i due termini e si traccia una linea;

- si moltiplica ciascuna cifra del secondo fattore per il primo fattore;

- si scrive il risultato del primo prodotto e si cambia di volta in volta riga per riportare gli altri ricordando di lasciare un posto vuoto sotto la prima cifra a destra di ciascun risultato;

- si sommano i vari risultati ottenuti.

Esempi di prodotto tra numeri binari

\( \bullet \ (110)_2 \times (10)_2 \ = \ \mbox{?} \)

\( \begin{array}{c c c c c c} & 1 & 1 & 0 & \times & \\ & & 1 & 0 & = & \\ \hline & 0 & 0 & 0 & + & \to 110 \times 0\\ 1 & 1 & 0 & & = & \to 110 \times 1 \\ \hline 1 & 1 & 0 & 0 & \end{array} \)

Quindi \( (110)_2 \times (10)_2 \ = \ 1100 \)

\( \bullet \ (101)_2 \times (110)_2 \ = \ \mbox{?} \)

\( \begin{array}{c c c c c c c} & & 1 & 0 & 1 & \times & \\ & & 1 & 1 & 0 & = & \\ \hline & & 0 & 0 & 0 & + & \to 101 \times 0\\ & 1 & 0 & 1 & & + & \to 101 \times 1 \\ 1 & 0 & 1 & & & = & \to 101 \times 1 \\ \hline 1 & 1 & 1 & 1 & 0 & \end{array} \)

Ovvero \( (101)_2 \times (110)_2 \ = \ (11110)_2 \)

Rapporto tra numeri binari

La divisione tra numeri binari è senza dubbio la più difficile tra le 4 operazioni aritmetiche e si entra spesso in confusione perché siamo abituati a pensare utilizzando il sistema di numerazione decimale. Per ovviare a questo inconveniente vediamo un esempio proponendoci di calcolare la divisione tra (10010)₂ e (10)₂.

Scriveremo una serie di passaggi che, se seguiti passo passo, non lasceranno spazio ad errori. 

1. si incolonnano i due numeri da dividere (dividendo e divisore) così come visto per i numeri naturali;

   \( \begin{array}{c c c c c | c c} 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ \hline &&&&& \\ &&&&& \end{array} \)

2. si prende, nel dividendo, un gruppo di cifre tali da avere un numero maggiore o uguale al divisiore contrassegnandole con una linea;

   \( \begin{array}{c c c c c | c c} 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ \hline &&&&& \\ &&&&& \end{array} \)

3. poiché stiamo lavorando nel sistema binario, si possono utilizzare solo le cifre 0 e 1; inoltre poiché un numero non può iniziare per 0, la prima cifra del quoziente sarà necessariamente 1. Riporteremo quindi un 1 come prima cifra del risultato;

   \( \begin{array}{c c c c c | c c} 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ \hline &&&&&1 \\ &&&&& \end{array} \)

4. si moltiplica il divisore per 1 (ottenendo, ovviamente, il divisore stesso) e lo si riporta sotto alle cifre contrassegnate del dividendo;

   \( \begin{array}{c c c c c | c c} 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ \hline 1&0&&&&1 \\ &&&&& \end{array} \)

5. si esegue la sottrazione tra i due numeri;

   \( \begin{array}{c c c c c | c c} 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ \hline 1&0&&&&1 \\ \hline =&=&&&& \end{array} \)

6. si scrive accanto al risultato della sottrazione la cifra successiva del dividendo;

   \( \begin{array}{c c c c c | c c} 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ \hline 1&0&&&&1 \\ \hline =&=&0&&& \end{array} \)

7. se il numero così ottenuto è maggiore del divisore si riporta un altro 1 nel quoziente, se è minore si riporta uno zero (nel nostro caso riporteremo quindi uno 0);

   \( \begin{array}{c c c c c | c c} 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ \hline 1&0&&&&1&0 \\ \hline =&=&0&&& \end{array} \)

8. si esegue la moltiplicazione tra il nuovo numero scritto e il divisore e lo si riporta nella colonna di sinistra (10 × 0 = 0)

   \( \begin{array}{c c c c c | c c} 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ \hline 1&0&&&&1&0 \\ \hline =&=&0&&& \\ & & 0 & & &\end{array} \)

9. si procede come visto nei punti 5) - 8) fino a quando non terminano le cifre del dividendo;

   \( \begin{array}{c c c c c | c c c c} 1 & 0 & 0 & 1 & 0 & 1 & 0 \\ \hline 1&0&&&&1&0&0&1 \\ \hline =&=&0&&& \\ & & 0 & & & \\ \hline & & = & 1 & \\ & & & 0 & \\ \hline & & & 1 & 0 & \\ & & & 1 & 0 & \\ \hline & & & = & = \end{array} \)

Possiamo quindi concludere che \( (10010)_2 : (10)_2 = (1001)_2 \ \mbox{resto} \ 0 \)

Altro esempio di divisione nel sistema binario

\( \bullet \ (10001)_2 : (11)_2 = (101)_2 \ \mbox{resto} \ 10 \), infatti, procedendo come appena visto:

\( \begin{array}{c c c c c | c c c} 1 & 0 & 0 & 0 & 1 & 1 & 1 \\ \hline &1&1&{\color{red}\downarrow}& {\color{blue}\downarrow}&1&0&1 \\ \hline =&=&1&0&{\color{blue}\downarrow}& \\ & & 0 & 0 & {\color{blue}\downarrow}& \\ \hline & & 1 & 0 & 1 \\ & & & 1 & 1 \\ \hline & & & 1 & 0 & \end{array} \)

dove abbiamo considerato dapprima (100)₂ essendo (10)₂ < (11)₂ \( Wink \)